Swinging Physics: The Answers
Fall
2015
Physics Puzzler
Swinging Physics: The Answers
Donald Simanek, Professor Emeritus, Lock Haven University of Pennsylvania

The period of the swing is the same as that of a simple pendulum of length R, where R is the length of the supporting ropes. The parallel rope suspension allows the chair to swing without rotation. Therefore each and every little piece of the chair swings in an arc of the same radius. Imagine all of these pieces separated, swinging in synchronism. Each would have period T = 2π√(R/g), where R is the radius of the arc of motion of each piece. So the entire porch swing also has that period—the period of a simple pendulum. In fact, an object of any shape and mass suspended from three or four parallel ropes of equal length also has the same period.
Such parallel suspension ensures that the object swings but does not rotate. The period is the same for forward swinging or side-wise swinging, or even swinging in an oval path. This can be thought of as a superposition of left-right and forward-back motions of the same period. And the period is independent of the mass on the swing.
But if the suspension ropes are nonparallel, some interesting motion results. A flat plate suspended by two ropes on either side that meet at the ceiling can swing with a rocking motion. Definitely not elementary, but quite relaxing. In fact, this could easily lead us to suspensions causing gentle rocking, as in the piece of furniture known as the platform rocking chair.
In this solution we have used the same argument that Galileo used to conclude that the time it takes a body to fall a given distance is independent of the body’s mass. He imagined dropping two identical bodies side by side, close to one another. Being identical, they take the same time to fall. Fasten them together and they still take the same time, though now the composite body has twice as much mass.
Another neat application of this principle is to explore something seldom proven in elementary physics textbooks. Why is the period of a simple pendulum (moving in a vertical plane) independent of its mass? Imagine two identical simple pendulums swinging side by side in synchronism. Of course their periods are the same since they are identical. Now bring them close together side by side, so the pendulum bobs are nearly touching. Both periods are still the same. Now glue the bobs together so they are, in effect, one pendulum. The period of this composite body is still the same, though it is twice the mass of either of the original pendulums, illustrating that the period of a simple pendulum is independent of the mass.
The argument still requires that we show the generality of the result. Imagine splitting a pendulum bob into two equal parts. Each has the same period. Three equal parts, same period. N parts ... same period. Small bobs can be recombined in whatever ways are required to make pendulums of different masses all with the same period.
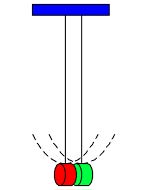 This works even if the pendulum bobs are large, so long as both bobs swing in exactly the same way, that is, along the same arc. And it even works if the angle of the swing is large. If the individual pieces didn’t swing in an arc of the same radius, gluing them together would result in a swing around some other arc, with a different period. This reminds us that the R in the formula for a simple pendulum is the radius of the arc of the bob’s motion, not simply the suspension length. A mass sliding on a frictionless track curved in the same circular arc would have the same period. Textbooks somewhat mislead by using L in the formula for the period, implying the length of the supporting string. The pendulum with a string support is only a special case.
This works even if the pendulum bobs are large, so long as both bobs swing in exactly the same way, that is, along the same arc. And it even works if the angle of the swing is large. If the individual pieces didn’t swing in an arc of the same radius, gluing them together would result in a swing around some other arc, with a different period. This reminds us that the R in the formula for a simple pendulum is the radius of the arc of the bob’s motion, not simply the suspension length. A mass sliding on a frictionless track curved in the same circular arc would have the same period. Textbooks somewhat mislead by using L in the formula for the period, implying the length of the supporting string. The pendulum with a string support is only a special case.
If you would like more rigorous proof, you can derive the period starting with conservation of energy. //
Share Your Photos
Email sps-programs [at] aip.org a photo of your chapter exploring porch swing physics, and you could be featured in the next issue of The SPS Observer!
Contact SPS
Have thoughts on this puzzle? Send them to us at sps-programs [at] aip.org.