Strange Consequences of the Finite Speed of Light
Spring
2015
Elegant Connections in Physics
Strange Consequences of the Finite Speed of Light
Dwight E. Neuenschwander, Professor of Physics, Southern Nazarene University, Bethany, OK
Because the speed of light is finite, we never see things as they are, but only as they were. In a sense, we are always looking at the past; information from the past comes swiftly to us in the form of light. Sometimes it’s interesting to stop and recollect our thoughts on points of physics we know well to appreciate how strangely interesting they reveal the world to be.
The special theory of relativity inverted Newtonian paradigms of space, time, and light. In Newtonian relativity, space and time were separately invariant; consequently, the speed of light was relative. Furthermore, time was independent of the three spatial dimensions, so time in the Newtonian world had no “direction.” In contrast, special relativity postulates the speed of light to be invariant; as a result, space and time are relative and form a four-dimensional geometry, giving time a direction in space-time. According to Hermann Minkowski, one of Einstein’s professors, mathematicians should have anticipated the hyperbolic geometry of space-time and been the ones to invent special relativity. Three years after Einstein published “On the Electrodynamics of Moving Bodies,” Minkowski delivered a speech called “Space and Time” to the 80th Assembly of German Natural Scientists and Physicians:[1]
…We will try to visualize things by the graphic method. Let x, y, z be rectangular coordinates for space and let t denote time. The objects of our perception invariably include places and times in combination. Nobody has ever noticed a place except at a time, or a time except at a place….With this most valiant piece of chalk I might project upon the blackboard four world-axes. Since merely one chalky axis, as it is, consists of molecules all a-thrill, and moreover is taking part in the Earth’s travels in the universe, it already affords us ample scope for abstraction…
…The concepts, space and time, cause the x, y, z-manifold t = 0 and its two sides t > 0 and t < 0 to fall asunder….To establish this connection, let us take a positive parameter c, and consider the graphical representation of
c2 t2 – x2 – y2 – z2 = 1. (1)
It consists of two surfaces separated by t = 0, on the analogy of a hyperboloid of two sheets. We consider the sheet in the region t > 0, and now take those homogeneous linear transformations of x, y, z, t into four new variables x', y', z', t' for which the expression for this sheet in the new variables is of the same form…
On his diagram Minkowski constructs new x'-t' axes (suppressing y and z) that preserve the form of the hyperbola in Eq. (1). All such transformations parametrized by c form a group that he calls Gc . As c approaches infinity, the new x' axis approaches the old x axis, and the direction of the t' axis—the “direction of time”—becomes ill defined. Thus, continues Minkowski,
…The group G∞, becomes no other than the complete group which is appropriate to Newtonian mechanics. This being so, and since Gc is mathematically more intelligible than G∞, it looks as though the thought might have struck some mathematician, fancy-free, that after all, as a matter of fact, natural phenomena do not possess an invariance with the group G∞, but rather with a group Gc, c being finite and determinate, but in ordinary units of measure, extremely great. Such a premonition would have been an extraordinary triumph for pure mathematics. Well, mathematics, though it now can display only staircase wit, has the satisfaction of being wise after the event, and is able, thanks to its happy antecedents, with its senses sharpened by an unhampered outlook to far horizons, to grasp forthwith the far-reaching consequences of such a metamorphosis of our concept of nature.
I will state at once what is the value of c with which we shall finally be dealing. It is the velocity of light in empty space.
Because the speed of light is “exceedingly great,” in everyday life we get away with treating it as if it were infinite. When the referees in a football game review the replay video of the game-winning touchdown that was thrown as the game clock reached 00:00, they do not worry about the time required for the light to travel to the various cameras. Those time intervals are so short—about 30 nanoseconds for a camera 10 meters from one of the crucial events—as to be indistinguishable from zero. One exception in daily life is the noticeable delay in conversations via satellite between parties on opposite sides of the world. For the signal to travel 60,000 miles or so takes about a third of a second. But whether it makes a practical difference in routine life or not, when I look at you across the coffee-shop table, the realization that I see you not as you are but as you were a nanosecond ago nurtures a deeper appreciation for how the world works.
When the distance scales are vaster than those of daily life, the strangeness of the world becomes significant. Traversing astronomical distances lies outside our store of personal experiences, but we can appreciate the issues by using familiar distances while imagining the speed of light to be slow enough that the consequences would become part of our tacit knowledge.[2] For example, where I live in Oklahoma places me about 1,500 miles from Appomattox, Virginia, where in 1865 General Robert E. Lee surrendered to General Ulysses S. Grant to end the American Civil War. I am writing this in 2015, the 150th anniversary of the Appomattox surrender. Supposing the speed of light were only 10 miles per year (kindly ignore all other changes to the world that would result from such a ridiculous scenario), the light from the Appomattox surrender—the fastest way information could travel—would just now be entering my telescope in Oklahoma. If I knew from earlier telescopic observations who Lee and Grant were, I could announce “News flash—General Lee has just surrendered to General Grant!” Such exaggerated examples (which have pedagogical uses when teaching introductory astronomy) illustrate the limits placed on the exchange of information by the finite speed of light.
I am sitting outside in my backyard on a beautiful starry night. For the sake of illustration, let me use round numbers. Suppose the Moon is about two light-seconds away, Jupiter about 30 light-minutes away, and Sirius about 8 light-years from Earth—not to mention the Andromeda galaxy about two million light-years from us, and that’s only the galaxy next door. At this moment now, light from each of these bodies arrives here, simultaneously, where I sit on my patio. The light entering my eye at this now moment (like the moment a photograph is taken with a superfast shutter speed) bounced off the lunar surface two seconds ago; the light arriving now from Jupiter reflected off the Jovian upper cloud deck half an hour ago; and the photons now arriving from Sirius left that blue giant’s surface eight years ago. If I plot on a space-time diagram (not to scale!) the emission events of all those signals and my reception of them here and now, I make something like Fig. 1.
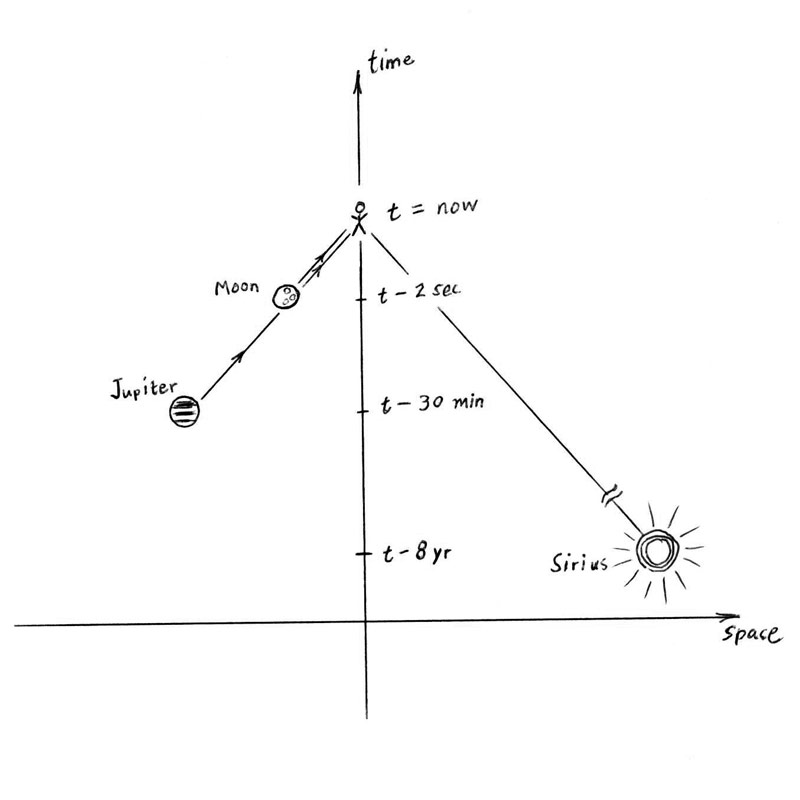
We realize as we gaze at the sky at this moment that we are seeing the Moon, Jupiter, and Sirius not as they are, but as they were, two seconds, half an hour, and eight years ago, respectively. What’s happening at Sirius now we have no way of knowing; if it exploded tonight we could not know it for another eight years—the last bit of light emitted is just now setting out on its way, and its trailing edge has to travel 8 light-years to reach my patio.
Light arriving here at tonight’s now moment also includes the microwave photons from the cosmic background radiation, when those photons last Thompson-scattered off the gas of ionized atoms and free electrons, around 400,000 years after the big bang. At that time the primordial fireball became cool enough for electrons to stay bound to nuclei, forming neutral atoms and allowing light to propagate freely across the universe, the big bang’s afterglow. The same thing happened here 13.7 billion years ago, but the Thompson-scattered photons that were the last to be scattered at the chunk of space where I now sit are, tonight, 13.7 billion years removed, heading away from here, while their fellows from across the universe, going the opposite direction, are intercepted here by us tonight. Mind-blowing events sometimes offer material for lofty thoughts.
The finite speed of light presents serious challenges for space travel and communication. At the speed of a commercial airliner, the time to travel between the Sun and Earth would be 17 years. To go from the Sun to Jupiter would take about 89 years. Traveling from the Sun to Alpha Centauri, 4.2 light-years distant, would take about 4.6 million years. To cut the flight time to something reasonable, we obviously must go much faster. But E = mc2(1 – v2/c2)–½ means that enormous amounts of energy are required for a spacecraft to travel a significant fraction of the speed of light. For example, a 100-ton spacecraft moving at half the speed of light represents a kinetic energy of about 1022 J. In recent years the United States consumed approximately 1020 J annually.[3] Thus the kinetic energy represented by such a boost of this payload would be a hundred times the annual energy consumption of the USA. Although this problem is solvable in principle, it does present daunting engineering and economic challenges.[4]
Radio communications between mission control and its spacecraft face interesting delays, as NASA engineers well know from keeping in touch with Mars rovers, the Cassini mission to Saturn, the Voyager probe now leaving the solar system, and so on. If you tell a Mars rover to turn left, it won’t receive your command for at least four to twenty minutes, depending on the locations of Earth and Mars in their orbits about the Sun. When driving Spirit and Opportunity, speeding is not allowed.
If other star systems are home to civilizations capable of communicating by radio, making contact with them is also a matter of timing. We have been broadcasting radio programs for about a century and television programs for over half a century. Imagine an episode of I Love Lucy broadcast in 1955. Some of that radiated signal leaked past the ionosphere into interstellar space and would now be 60 light-years from Earth. If a civilization within that range has a sufficiently sensitive receiver tuned to the right frequency, they might pick up the faint signal and amplify it (if they are able to filter the program from the carrier wave). Whether they would conclude it was sent by intelligent life forms another question. If they are just now detecting it and decide to reply at once, we won’t receive their reply for another 60 years. A spherical shell with a 60 light-year radius encloses about 900,000 cubic light-years. If we assume 4 light-years of distance between stars in our corner of the galaxy to be typical, so that a 4×4×4 cubic light-year volume selected at random in a neighborhood holds about four stars, then this back-of-the-envelope calculation suggests that the 1955 I Love Lucy episode has swept over something on the order of a hundred thousand stars. If only one percent of them have an Earth-like planet in a star’s habitable zone, that’s still on the order of a few thousand potential extrasolar viewers of Lucy’s antics. Was anyone out there tuned in?
How long will a transmitting civilization be able to broadcast signals, and how long will the receiver civilization be capable of receiving them? Since radio broadcasting technology develops approximately coincidentally (on an evolutionary timescale) with nuclear weapons and with industries that destroy the ecosystem faster than the users realize what they are doing, we have no guarantee that, once a civilization becomes radio communicative, it won’t destroy itself on a timescale short compared to astronomical light-travel times. Picture interstellar radio broadcasts as arrows traveling outward in all directions from the sending planet. If a civilization broadcasts for a time equal to 100 Earth years, those arrows are 100 light-years long. For our colleagues in the Search for Extraterrestrial Intelligence (SETI) to detect a signal from an extrasolar civilization, the SETI listeners must have their “ears on” some time while that arrow transmitted by the other civilization sweeps over the SETI antennas. If a receiver’s star can support a habitable planet for five billion years after the resident civilization becoming technological, but the sending civilization transmits radio signals for only a thousand years, then during the remaining lifetime of the receiver’s star, the odds that the receiver’s antenna will happen to be on during the time the sender’s arrow sweeps through the receiver’s solar system is about one chance in five million.
Because of the finite speed of light, not only do we see events after they happen and objects as they used to appear, but we also see the shapes of objects distorted. The effects I mean are not those of relativistic length contraction. Special relativity deduces from its postulates a distinction between an object’s “proper length” Lo (its length measured when at rest) and its length L when it moves by the observer with speed v (the time between the moving object’s front and back edges passing a fixed marker, measured with a local clock at the marker). The proper and “improper” lengths are related by the length contraction formula, L = Lo(1 – v2/c2)½. Students frequently ask, “What is the actual length?” but that is not the question. The length of an object is not a property of the object itself; rather, length is a relationship between observer and observed, and that relationship depends on their relative motion. Both L and Lo are “actual” lengths.
The focus of our attention here is not proper versus contracted length, but how the object visually appears because of the time required for the signal to travel between source and observer. Stand with me by the narrow-gauge railroad track near Durango, Colorado, as the magnificent antique steam locomotive No. 478 of the Durango & Silverton Railroad comes thundering down the track (Fig. 2).

It left Durango a few minutes earlier, and as it comes toward us it’s up to speed and heading toward Red Mountain Pass en route to Silverton. I am standing with you alongside the track, looking down the length of the entire train, seeing in one glance everything from the headlight on the locomotive to the caboose. At time t, which means the now moment (like snapping a photograph with a superfast shutter), some of the light entering my camera came from the locomotive’s headlight and some of it came from the caboose; that is why I can see the entire train at time t = now (assuming parallel rays). Because the train is moving with velocity v and because the speed of light is finite, in principle the train appears longer than the train’s measured length L. (L is already length-contracted relative to the proper length.) Let L' be this visual length.
For the light that reflected off the caboose and the light emitted by the headlight to enter my camera together at time t = now, the photon from the caboose had to come alongside the headlight at the same instant the headlight emitted its photon. After that the two photons travel side-by-side to enter my camera simultaneously. After leaving the caboose, the caboose photon had to catch up with the front of the train and thus traveled the distance (relative to me) L’, which takes time (as seen by me) Δt; therefore L' = cΔt. Meanwhile, the front of the train moved the distance vΔt. Thus to catch the headlight the caboose photon had to travel the length L' = L + vΔt = L + v(L’/c) so that L' = L(1 – v/c)−1. Generalized to three dimensions, a visual volume V' compares to the measured volume V according to
(2)
where R is the vector from a source point to the observer.
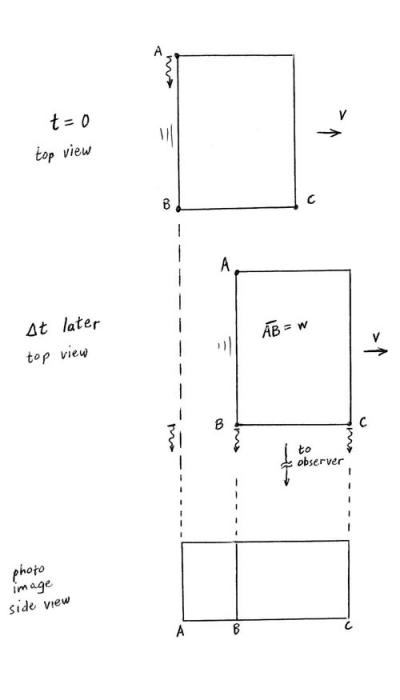
For a similar reason, a three-dimensional object sweeping by an observer will appear rotated.[5] Consider a box moving with velocity v past an observer. Let the box’s plane nearest the observer be parallel to the direction of v. The issue here is not the change in shape or volume due to length contraction; rather, the point of interest here is how the box appears rotated because of the extra time it takes for light from the far trailing edge to traverse the box’s width. Let A denote the far trailing edge, and let B and C denote, respectively, the trailing and leading edges of the box face closest to the observer (Fig. 3). The light from A, B, and C that arrives simultaneously at the observer’s camera had to cross the B-to-C line together (assuming the photographer to be far enough away that light rays from A, B, and C are parallel when they enter the shutter). That means the light from A had to leave at time Δt = w/c earlier than the light from B and C, where w denotes the A-to-B length. In that time B and C move the distance vΔt to the observer’s right. Although the A, B, and C photons cross the B-C line together, the photon from B will have departed to the right of the A photon, so in the photograph the back side of the box appears to the observer to have been rotated through an angle θ, where sin θ = vΔt/w = v/c.
KEEP READING
The finite speed of light also has profound implications for electromagnetism. To learn more, read the second part of this article online here.
Acknowledgments
Thanks to Daniel Golombek for some very helpful suggestions. I wish to express gratitude to my electrodynamics professors who opened new doors of appreciation to me, Richard Jacob and the late Sallie Watkins.
[1] Hermann Minkowski, “Space and Time,” speech of September 21, 1908, reprinted in The Principle of Relativity (Dover Publications, General Publishing Co., 1952), 76–79.
[2] George Gamow was good at this kind of explanation; see his Mr. Tomkins in Paperback (Cambridge Univ. Press, London, UK, 1967), Ch. 1, “City Speed Limit.”
[3] U.S. Energy Information Administration, http://www.eia.gov/consumption/.
[4] For a detailed account of a serious attempt to use small nuclear bombs to propel a spacecraft, see George Dyson, Project Orion: The True Story of the Atomic Spaceship (Henry Holt and Co., New York, NY, 2002).
[5] See, for example, Richard T. Weidner and Robert L. Sells, Elementary Modern Physics (Allyn & Bacon, Boston, MA, 1973), 67–68.
Pdf issue
Strange Consequences of the Finite Speed of Light - Part 2 - online only
